ABCD es un paralelogramo con P y Q como puntos medios…

Sea ABCD es un paralelogramo con P y Q como puntos medios de los lados BC y CD respectivamente. Demuestre que AP y AQ trisecan la diagonal BD en los puntos E y F.

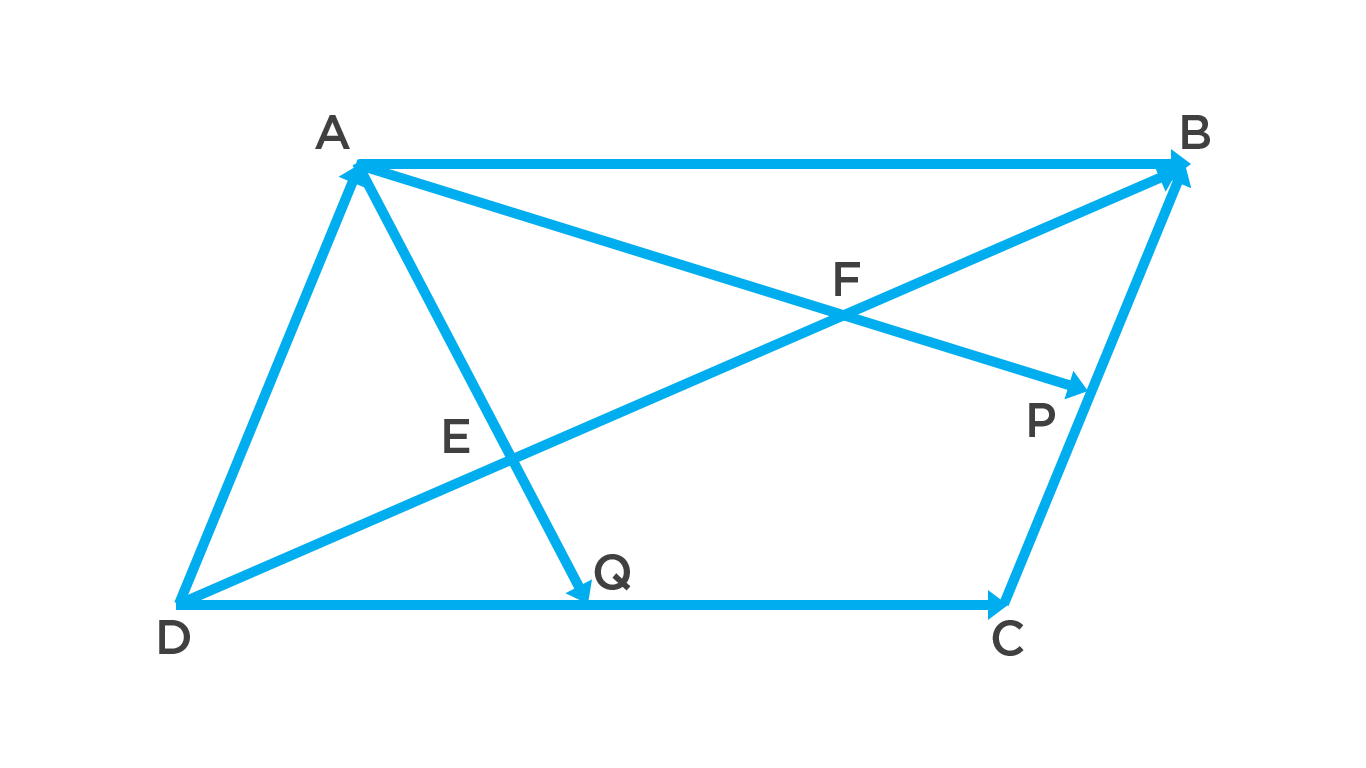
Ejercicio 1.44 de la segunda edición del libro de Análisis Vectorial de Schaum. Para demostrar este ejercicio, voy a utilizar dos teoremas:

Las diagonales de un paralelogramo se cortan en su puntos medios

Las medianas de un triángulo se trisecan

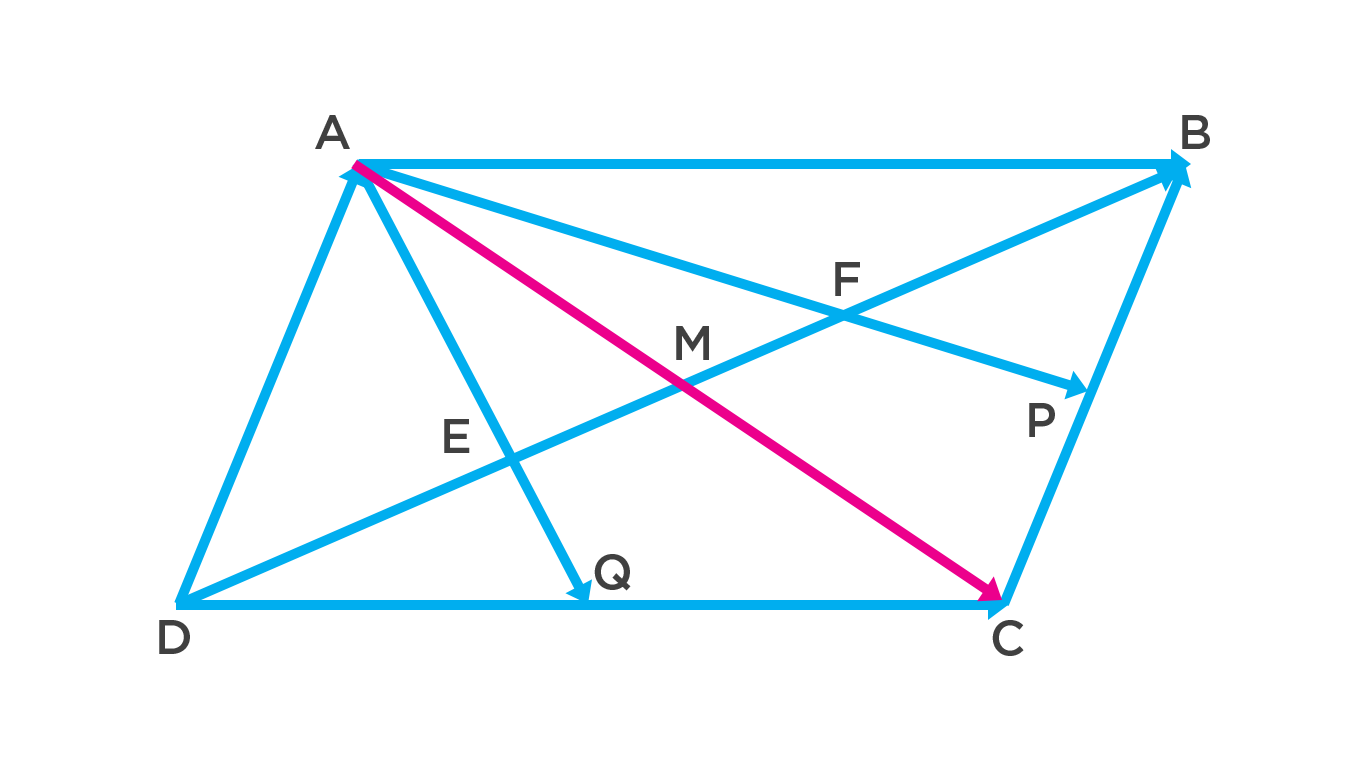
Al trazar la diagonal faltante AC, podemos dividir el paralelogramo en dos triángulos, uno formado por los puntos ADC y el otro por ACB.

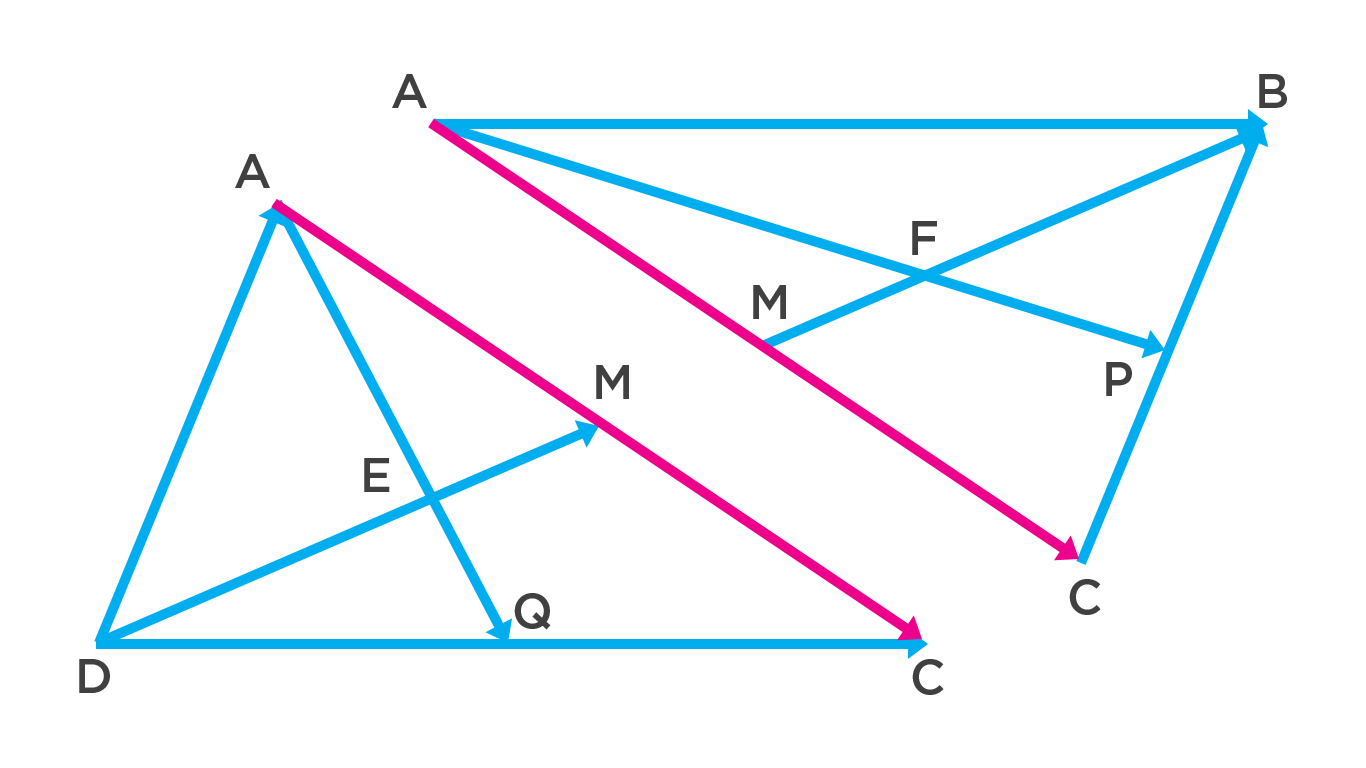
Los vectores DM y AQ son medianas del triángulo ADC, usando el teorema 2, E es el punto donde las medianas se cortan y además, se cortan en una tercera parte de su longitud, dicho de otra manera, el lado más largo de la mediana mide 2 veces el lado más corto.

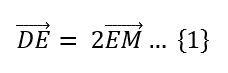
Siguiendo el mismo razonamiento, para el triángulo ACB, tenemos que:

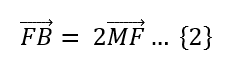
La diagonal DB es la suma de DM con MB:

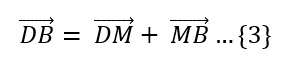
Las diagonales de un paralelogramo se cortan en sus puntos medios, lo que implica que:

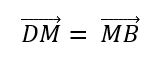
Luego:

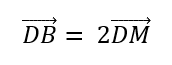
Además, DM se compone de otros vectores:

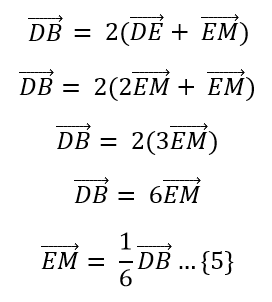
Finalmente, por la ecuación 1:

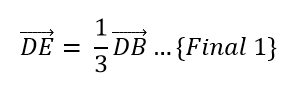
Por la ecuación 4:

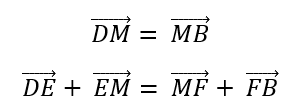
Por las ecuaciones 1 y 2:

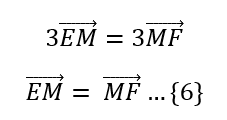
Usando la ecuación 6 con 5:

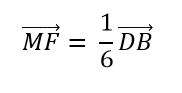
Ayudándonos con la ecuación 2:

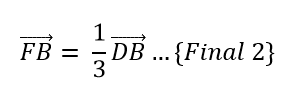
De las ecuaciones Final 1 y Final 2:

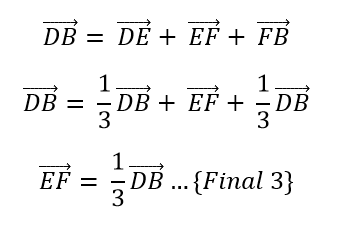
Recapitulando, de las ecuaciones Final 1, Final 2 y Final 3, ya que DE, EF y EB son iguales y sumados obtenemos DB, entonces podemos concluir que E y F trisecan a la diagonal DB.

Publicado por Julio Montaño el 14/Ene/2013.