Demostrar que las diagonales de un paralelogramo se cortan en sus puntos medios

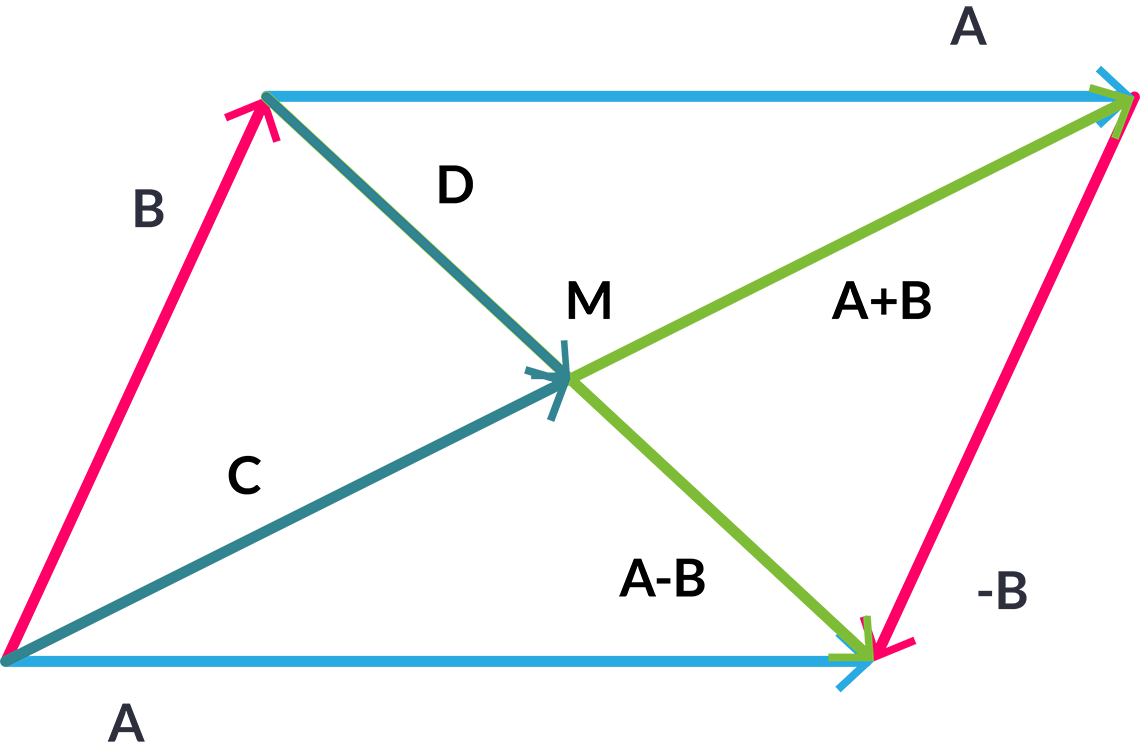
Supongamos que tenemos dos vectores diferentes, A y B, y que estos vectores parten del mismo punto, ya que podemos trasladar vectores sin problema alguno, lo hacemos para obtener un paralelogramo, cuyos lados son A y B y sabemos que es un paralelogramo porque el vector A siempre conserva su dirección, hacemos lo mismo con B.

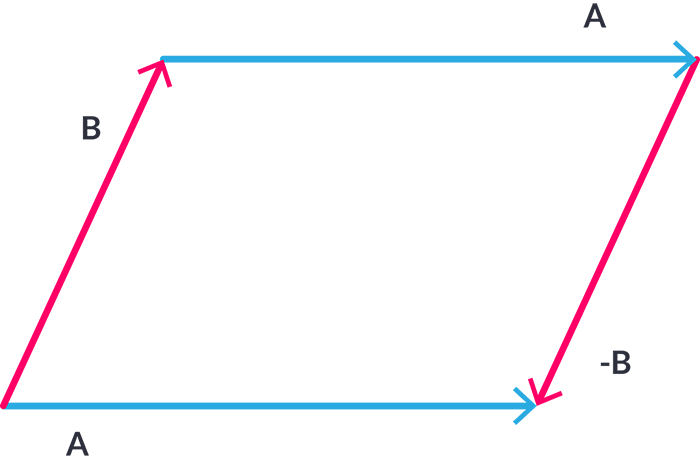
Una diagonal, es una linea (o también un vector) que va de un punto a otro en una figura, estos puntos tienen que ser vértices de la figura y no tienen que ser consecutivos o adyacentes. En un paralelogramo de 4 lados, tenemos 2 vértices, trazándolos en el paralelogramo podemos observar que las diagonales son la suma de los vectores.

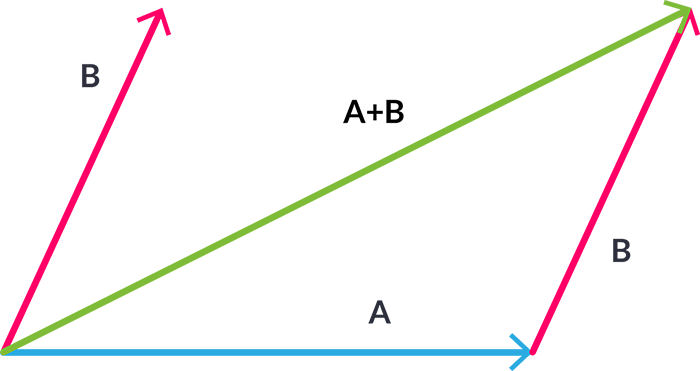
En la imagen anterior se puede observar que estoy desplazando el vector B, para sumarlo con A, después, el vector que representa la suma es A+B, a ésta diagonal la llamaré F.

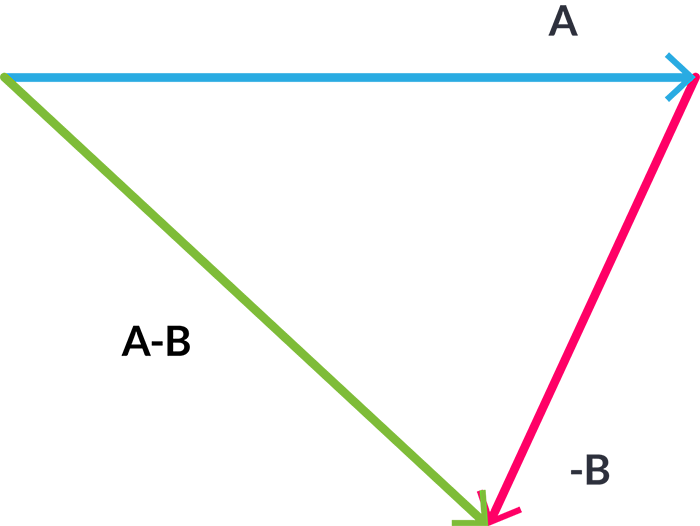
Para la otra diagonal, necesito sumar a A con -B, a ésta la llamaré G.

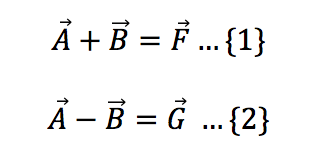
De las ecuaciónes 1 y 2, despejaré al vector B para obtener las ecuaciones 3 y 4 respectivamente, nota que en 4, tenemos -B, si multiplicamos por -1 toda la ecuación, podemos reescribirla sin afectarla.

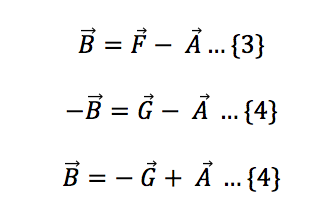
En las ecuaciones 3 y 4 tenemos a B despejado, y como B=B, podemos igualar las ecuaciones 3 y 4, o dicho de otra manera, sustituimos el valor de cualquier B en la otra ecuación, que queda expresado en la ecuación 5.

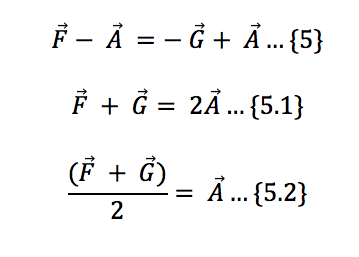
La ecuación 5.3 nos dice que A es la suma de las mitades de los vectores F y G, que son precisamente, nuestras diagonales y ya está, hemos resuelto el problema.

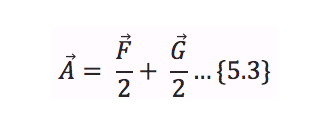
Si no lo entendiste aún, te continúo explicando: A la mitad del vector F le llamaré C y a la mitad de G, le llamaré D.

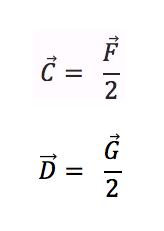
Sustituyendo (o cambiando simplemente los nombres), tenemos que A=C+ D.

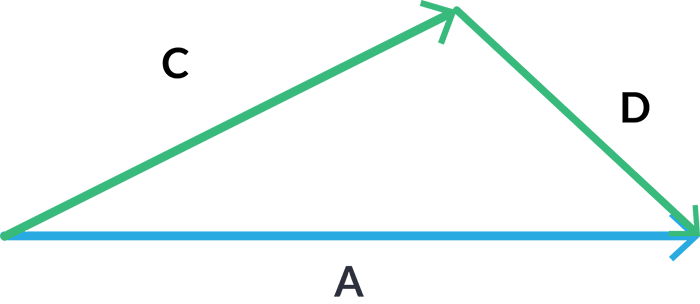
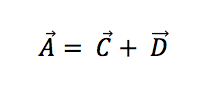
C es la mitad de F y D es la mitad de G, el punto donde se cruzan las diagonales es el punto donde se cruzan F y G, ese punto lo podemos notar como el punto donde termina C y empieza D, ese punto M es donde se intersectan las diagonales y el álgebra lo dice, se cortan en us puntos medios o se bisecan.

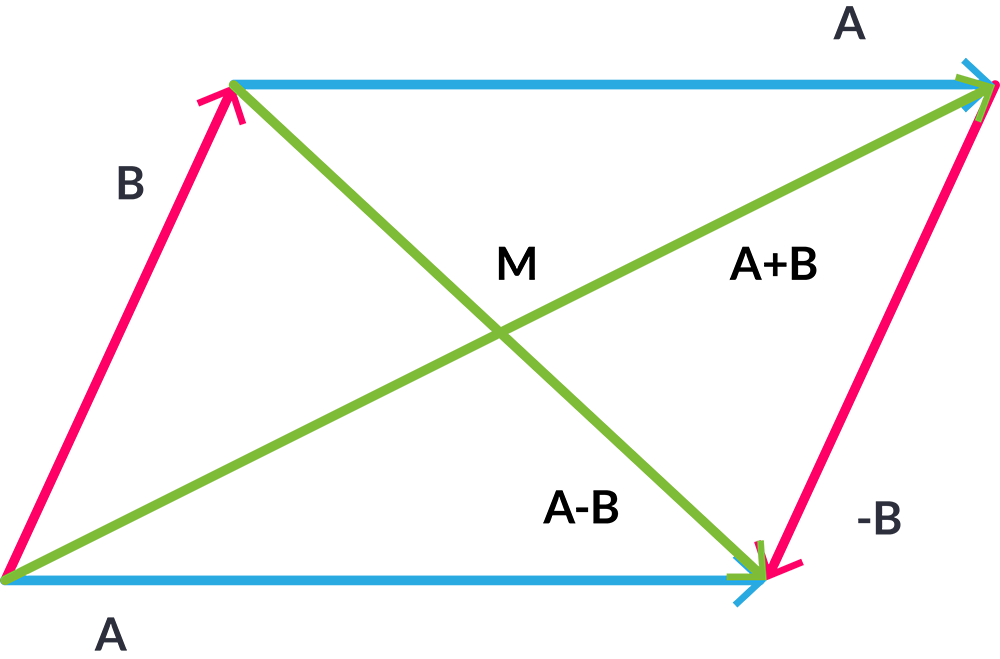
Otra forma de entender el problema es pensar en el punto M, M es el punto que existe en F y en G, F corta a G en el punto M y viceversa, el punto M se obtiene en la ecuación 5.3, es donde se tocan o cruzan los vectores y es en el punto medio de cada diagonal.

Publicado por Julio Montaño el 18/May/2013.